今回はモデルの複雑さを評価する内容となります。
バイアス(Bias)
モデルの予測値の平均と真の値との差。
高バイアス:モデルが単純すぎて、真の関係を表現できていない(例:線形モデルで非線形データを扱う)。
→ アンダーフィッティングの原因。
📌 例:
真の関係が曲線なのに、直線で近似しようとする ⇒ いつもズレてしまう。
バリアンス(Variance)
- 学習データが少し変わったときに、モデルの予測がどれだけブレるか。
- 高バリアンス:モデルがデータに過剰に適合しており、新しいデータにはうまく汎化できない。
- → オーバーフィッティングの原因。
📌 例:
学習データにピッタリ合わせすぎて、新しいデータには不安定な予測をする。
ノイズ(Inducible Error)
データ自体に含まれる予測できないランダムな誤差。
どんなモデルでもこれはゼロにできない。
例:測定誤差、人の入力ミスなど。
バイアス-バリアンスのトレードオフ
- 一般に、モデルを複雑にするとバイアスが下がり、バリアンスが上がる。
- モデルを単純にするとバイアスが上がり、バリアンスが下がる。
🎯 目的:ちょうどよい「バイアスとバリアンスのバランス」を取って、汎化性能(新しいデータへの対応力)を高める。
応用で使われる場面
- モデル選択(線形回帰 vs 決定木 vs ニューラルネットなど)
- ハイパーパラメータ調整(木の深さ、正則化、学習率など)
- アンサンブル学習(バリアンスを下げるためにバギングなど)
演習
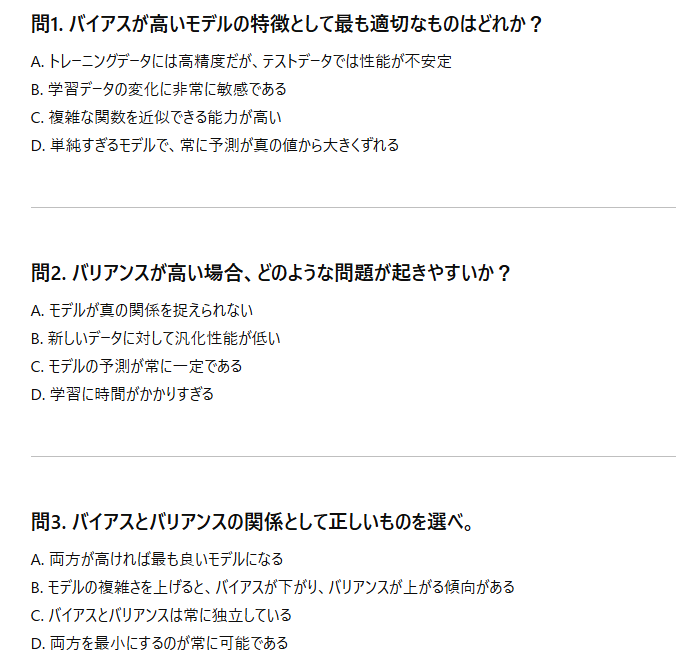
↓
↓
↓
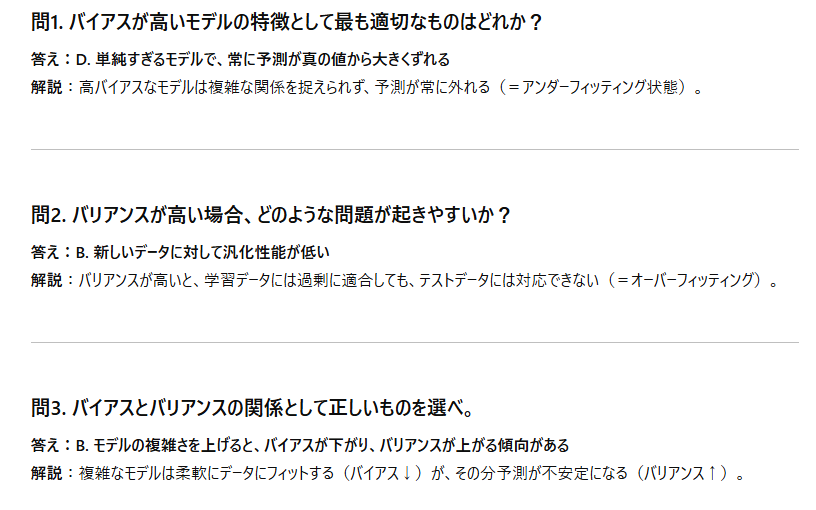
(解答)
参考資料
・データサイエンス数学ストラテジス