今回は複数の変数での関係を表現する内容となります。
重回帰分析(Multiple Linear Regression)
重回帰分析(Multiple Linear Regression, MLR) は、複数の説明変数(独立変数)を用いて、1つの目的変数(従属変数)を予測する手法。
単回帰分析では 1つの説明変数 を用いるが、重回帰分析では 2つ以上の説明変数 を用いる点が異なる。

重回帰分析の目的
重回帰分析は以下のような目的で利用されます。
- データの関係性の理解 :説明変数間の関係や、どの変数が重要かを調べる
- 目的変数の予測 :複数の要因から結果を予測する
- 説明変数の影響の測定 :各説明変数が目的変数にどれくらい影響を与えるか分析
回帰係数の求め方(最小二乗法)

決定係数R^2とモデルの評価

重回帰分析の注意点
重回帰分析を適用する際には、以下の点に注意する必要があります。
- 多重共線性(Multicollinearity)
- 説明変数同士が強い相関を持つと、回帰係数の信頼性が低くなる。
- 対策:VIF(分散膨張係数) を計算し、値が高い変数を削除・統合する。
- 過学習(Overfitting)
- 説明変数を増やしすぎると、訓練データには適合するが、新しいデータに対する汎化性能が低くなる。
- 対策:AIC・BICなどの情報量基準 を用いてモデルを適切に選択する。
- 外れ値の影響
- 極端な値(外れ値)があると、回帰係数が大きく影響を受けることがある。
- 対策:外れ値を取り除く、ロバスト回帰を使用する など
重回帰分析の応用例

まとめ

演習




↓
↓
↓
(解答)


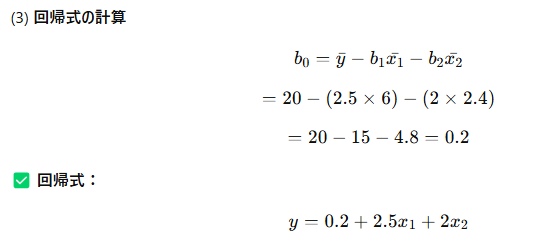


参考資料
・データサイエンス数学ストラテジス