今回はニューラルネットワークでの出力を変換する活性化関数に関する内容となります。
活性化関数(Activation Function)は、ニューラルネットワークにおいて、各ニューロンが出力を決定する際に使われる関数。入力信号を処理して、次の層へどのような信号を送るかを決める。活性化関数があることで、ネットワークは非線形な問題を解決できるようになる。
ステップ関数(Step Function)
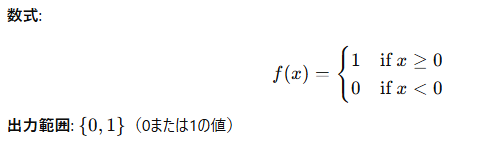
特徴:
ステップ関数は、入力が0以上なら1を、0未満なら0を返す単純な関数。出力が離散的なため、2クラス分類に使えることもある。しかし、勾配が不連続なため、バックプロパゲーションでの学習が困難(勾配消失問題)。そのため、深層学習ではあまり使われないが、初期のニューラルネットワークでは活用されていた。
シグモイド関数(Sigmoid Function)

特徴:
シグモイド関数は、S字型の滑らかな曲線を持ち、出力は0から1の範囲に収束する。主に二値分類問題で出力を確率として解釈するのに使用される。バックプロパゲーションでの勾配計算も可能だが、勾配消失問題が発生しやすいという欠点がある。これは、入力が非常に大きいか非常に小さい場合、勾配がほぼゼロになり、学習が進まなくなる原因である。
ReLU関数(Rectified Linear Unit)
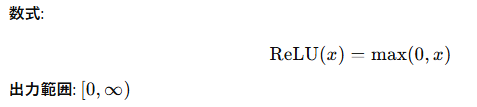
特徴:
ReLU関数は、入力が0以下の場合は0を、0より大きい場合はそのままの値を出力する関数。計算が非常に高速で、深層学習において非常に人気がある。ReLUの主な利点は、勾配消失問題を回避できることである。しかし、入力が常に負の値となると勾配がゼロになり、そのニューロンが「死んでしまう」現象(死んだReLU問題)が起こることがある。この問題を避けるために、Leaky ReLUやParametric ReLUといった改良版が提案されている。
各関数の比較
| 関数 | 特徴 | 利点 | 欠点 |
| ステップ関数 | 離散的な出力 (0または1) | シンプル、直感的 | 勾配消失問題、学習が遅い |
| シグモイド関数 | 出力が0から1の範囲 | 確率的な解釈ができ、二値分類に使用 | 勾配消失問題、学習が遅い |
| ReLU関数 | 0以下は0、それ以上はそのままの値を出力 | 計算が高速、勾配消失問題を回避できる | 死んだReLU問題、負の値に対応しない |
まとめ
・ステップ関数は、現在はほとんど使用されていないが、単純な二値分類などの初期のモデルで使用されていた。
・シグモイド関数は、出力が確率的で解釈しやすいため、主に二値分類の出力層で使用されるが、深層学習では勾配消失問題が課題となる。
・ReLU関数は、深層学習において最も広く使われており、計算が高速で、学習を効率化できるため、多くの隠れ層で使用される。しかし、死んだReLU問題に対処するために、Leaky ReLUや他の改良型が使われることがある。
・それぞれの活性化関数は、用途や問題に応じて適切に選択することが重要である。
演習
問題 1:
ステップ関数の特徴として正しいものはどれか?
- 出力が連続的で、勾配消失問題が発生しにくい。
- 出力が0または1で、非常に単純だが、勾配が不連続なため学習が困難。
- 出力が0から1の範囲に収束する。
- 入力が負の場合も値がそのまま通る。
問題 2:
シグモイド関数について正しい説明はどれか?
- 出力範囲が(−∞,∞)であり、負の値を出力する。
- 出力範囲が(0,1)であり、確率的な解釈が可能。
- 0以下の入力に対して、常に0を返す。
- 非線形性がないため、深層学習には向いていない。
問題 3:
ReLU関数の特徴として正しいものはどれか?
- 入力が0以下の場合もそのまま通し、負の値がそのまま出力される。
- 出力範囲が(0,1)であり、主に分類問題で使用される。
- 入力が0以下の場合は0を返し、それ以上の場合はそのままの値を返す。
- 勾配消失問題を引き起こすため、深層学習で使うのに適さない。
問題 4:
次のうち、深層学習でよく使われる活性化関数はどれか?
- ステップ関数
- シグモイド関数
- ReLU関数
- ハードサイン関数
問題 5:
ReLU関数の「死んだReLU問題」とは何か?
- 入力が非常に大きいため、勾配が消失して学習が進まない現象。
- ニューロンの出力が常に0になり、学習が進まなくなる現象。
- 出力が0または1に収束し、分類が進まない現象。
- 出力が0から1に収束せず、分類が不安定になる現象。
↓
↓
↓
(解答)
問1: ステップ関数の特徴
選択肢:
- 出力が連続的で、勾配消失問題が発生しにくい。
- 誤り: ステップ関数は離散的な出力を持つため、勾配が不連続で勾配消失問題が発生しやすいです。
- 出力が0または1で、非常に単純だが、勾配が不連続なため学習が困難。
- 正解: ステップ関数は0または1の出力で、勾配が不連続なため学習が困難になります。
- 出力が0から1の範囲に収束する。
- 誤り: ステップ関数は0または1という離散的な出力を返すため、連続的に範囲に収束しません。
- 入力が負の場合も値がそのまま通る。
- 誤り: ステップ関数は、入力が0未満の場合、出力が0となり、そのまま通すわけではありません。
問2: シグモイド関数の特徴
選択肢:
- 出力範囲が(−∞,∞)(-\infty, \infty)(−∞,∞)であり、負の値を出力する。
- 誤り: シグモイド関数の出力範囲は(0,1)(0, 1)(0,1)であり、負の値は出力されません。
- 出力範囲が(0,1)(0, 1)(0,1)であり、確率的な解釈が可能。
- 正解: シグモイド関数は出力が0から1の間に収束し、確率的な解釈が可能です(例えば、二値分類の出力)。
- 0以下の入力に対して、常に0を返す。
- 誤り: シグモイド関数は負の入力でも出力が0に近づきますが、0ではなく、0より大きな値を返します。
- 非線形性がないため、深層学習には向いていない。
- 誤り: シグモイド関数は非線形であり、深層学習でも使われますが、勾配消失問題があるため、近年ではあまり使用されません。
問3: ReLU関数の特徴
選択肢:
- 入力が0以下の場合もそのまま通し、負の値がそのまま出力される。
- 誤り: ReLU関数は、入力が0以下の値に対して0を返し、負の値は出力されません。
- 出力範囲が(0,1)(0, 1)(0,1)であり、主に分類問題で使用される。
- 誤り: ReLU関数の出力範囲は[0,∞)[0, \infty)[0,∞)であり、分類問題に特化したものではありません。
- 入力が0以下の場合は0を返し、それ以上の場合はそのままの値を返す。
- 正解: ReLU関数は、0以下の値に対して0を返し、それ以上の値についてはそのままの値を返します。
- 勾配消失問題を引き起こすため、深層学習で使うのに適さない。
- 誤り: ReLU関数は勾配消失問題を回避するため、深層学習で非常に多く使用されています。
問4: 活性化関数の選び方
選択肢:
- ステップ関数
- 誤り: ステップ関数は勾配消失問題が発生しやすいため、深層学習にはあまり使われません。
- シグモイド関数
- 誤り: シグモイド関数は勾配消失問題が発生するため、深層学習では近年使用が減っています。
- ReLU関数
- 正解: ReLU関数は計算が高速で、勾配消失問題を回避できるため、深層学習で非常に広く使われています。
- ハードサイン関数
- 誤り: ハードサイン関数は単純なステップ関数に近いもので、勾配消失問題を引き起こすため、深層学習で使われることは少ないです。
問5: ReLU関数の問題
選択肢:
1.入力が非常に大きいため、勾配が消失して学習が進まない現象。
誤り: これはシグモイド関数に関する特徴で、ReLU関数は勾配消失問題を回避します。
2.ニューロンの出力が常に0になり、学習が進まなくなる現象。
正解: ReLU関数の「死んだReLU問題」とは、入力が0以下の場合に出力が常に0となり、そのニューロンが学習しなくなる現象です。
3.出力が0または1に収束し、分類が進まない現象。
誤り: ReLU関数の出力は0またはそれ以上の値であり、0または1に収束するわけではありません。
4.出力が0から1に収束せず、分類が不安定になる現象。
誤り: これはシグモイド関数に関する特徴で、ReLU関数の出力は0以上の値を取ります。
参考資料
・データサイエンス数学ストラテジスト[上級]公式テキスト | 公益財団法人 日本数学検定協会 |本 | 通販 | Amazon