今回はニューラルネットワークでの教師データとの誤差を最小化する損失関数、勾配降下法に関する内容となります。
損失関数 (Loss Function)
損失関数は、モデルが予測した出力と実際のターゲット(正解ラベル)との誤差を定量化するための関数。モデルのパフォーマンスを評価するために使う。損失関数を最小化することが、機械学習モデルの学習過程の目標である。
一般的な損失関数
- 回帰問題: 予測値と実際の値の差を最小化することを目指す。代表的なものには以下の損失関数がある。
平均二乗誤差 (MSE, Mean Squared Error)
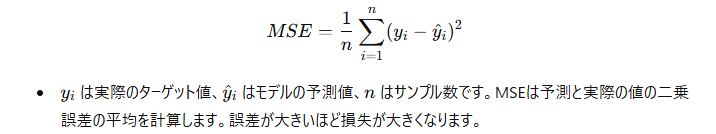
- 分類問題: クラス予測の誤差を最小化することを目指します。代表的なものには以下の損失関数があります。
クロスエントロピー損失 (Cross-Entropy Loss)
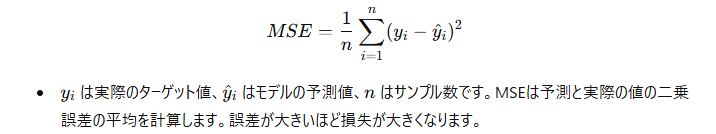
損失関数の目的
損失関数の目的は、モデルのパラメータ(重みやバイアスなど)を調整して、損失が最小になるようにすること。損失が小さいほど、モデルがターゲットに近い予測をしているということになる。
勾配降下法 (Gradient Descent)
勾配降下法は、最適なパラメータ(重みなど)を見つけるための最も広く使われている最適化アルゴリズム。モデルの損失関数を最小化するために、損失関数の勾配(微分)を計算して、その方向にパラメータを更新していく。
勾配降下法の基本的な考え方
勾配の計算: 損失関数をモデルのパラメータに関して微分します。これにより、損失関数がどの方向に増加または減少するかがわかります。
パラメータの更新: 勾配に反対方向にパラメータを調整して、損失を減らす方向に進みます。この調整量を学習率(Learning Rate)で決めます。
繰り返し: 上記の操作を繰り返し行い、損失関数が最小値に収束するようにパラメータを更新していきます。
勾配降下法の数式
最適化のために、パラメータ θを更新する数式は以下のようになります。

学習率 (Learning Rate)
学習率 ηは、パラメータの更新幅を決定します。学習率が大きすぎると、最適解を飛び越えてしまい、学習が不安定になる可能性がある。逆に、学習率が小さすぎると、学習が遅くなる。
勾配降下法の種類
勾配降下法にはいくつかのバリエーションがある。
1. バッチ勾配降下法 (Batch Gradient Descent)
- 特徴: すべてのデータを使って勾配を計算し、パラメータを一度に更新する。
- メリット: 安定して収束する。
- デメリット: 計算量が非常に多く、メモリを大量に消費する。
2. ミニバッチ勾配降下法 (Mini-Batch Gradient Descent)
- 特徴: データセットを小さなバッチに分けて、各バッチで勾配を計算しパラメータを更新する。
- メリット: 計算効率が良く、バッチ勾配降下法よりも早く収束する。適度にランダム性を持つため、局所解に陥るリスクが減る。
- デメリット: 依然として計算量が多くなる可能性がある。
3. 確率的勾配降下法 (Stochastic Gradient Descent, SGD)
- 特徴: 1つのデータサンプルを使って勾配を計算し、パラメータを更新する。
- メリット: 計算が非常に速く、大規模なデータセットに適している。ランダム性を持つため、局所解に陥るリスクがさらに低減する。
- デメリット: 更新がノイズを含むため、収束が不安定になることがある。
勾配降下法の改善手法
- モメンタム (Momentum): 勾配降下法に過去の更新情報を加えて、更新をスムーズにし、収束を加速する。
- Adam (Adaptive Moment Estimation): 勾配とその二乗を使って、学習率を適応的に調整する手法。勾配の変化が急激な場合に有効。
まとめ
- 損失関数は、モデルの予測誤差を評価するための関数。モデルのパラメータはこの損失関数を最小化するように更新される。
- 勾配降下法は、損失関数を最小化するために使用される最適化アルゴリズム。勾配を計算して、パラメータを更新することで学習を進める。
演習
問1:
次のうち、損失関数の役割として正しいものを選びなさい。
- モデルの予測値を最適な値に調整するための関数
- モデルの誤差を数値として評価する関数
- ニューラルネットワークの学習速度を決定する関数
- 勾配降下法の学習率を決める関数
問2:
次の記述のうち、誤っているものを選びなさい。
- MSE(平均二乗誤差)は、回帰問題によく使われる。
- クロスエントロピー損失は、分類問題でよく使われる。
- MSEは誤差の絶対値を使うため、負の誤差と正の誤差を区別できる。
- クロスエントロピー損失は、確率的な出力を前提とする。
問3:
勾配降下法において、パラメータ θの更新式として正しいものを選びなさい。

問4:
次の記述のうち、誤っているものを選びなさい。
- バッチ勾配降下法は、全データを使って勾配を計算するため、計算コストが高い。
- ミニバッチ勾配降下法は、データセットを小さなバッチに分割して学習するため、バッチ勾配降下法より計算効率が良い。
- 確率的勾配降下法(SGD)は、全データを一度に処理するため、収束が非常に速い。
- ミニバッチ勾配降下法は、バッチ勾配降下法と確率的勾配降下法の中間的な性質を持つ。
問5:
学習率(Learning Rate)に関する説明として、正しくないものを選びなさい。
- 学習率が大きすぎると、最適な解を飛び越えてしまい、収束しないことがある。
- 学習率が小さすぎると、収束が遅くなる可能性がある。
- 学習率は固定でなければならず、変化させると学習が不安定になる。
- Adamのような最適化手法は、学習率を適応的に調整する。
問6:
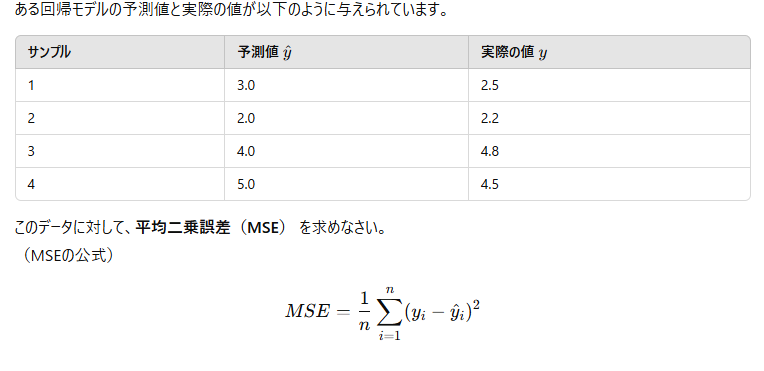
問7:

問8:
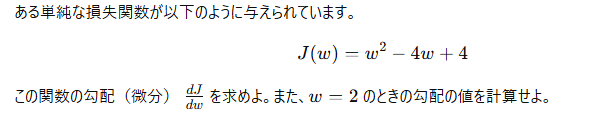
問9:

↓
↓
↓
(解答)
問1: 損失関数の役割 → ✅ 2
解説:
損失関数は、モデルの誤差を数値として評価する関数です。
- (1) 誤り: 損失関数は誤差を測るものであり、予測値を直接調整するわけではない。
- (3) 誤り: ニューラルネットワークの学習速度は、学習率(Learning Rate)によって決まる。
- (4) 誤り: 勾配降下法の学習率は、最適化アルゴリズムや設定値によって決まり、損失関数自体が決めるわけではない。
問2: MSEとクロスエントロピー損失 → ✅ 3
解説:
- (1) 正しい: MSE(平均二乗誤差)は回帰問題でよく使われる。
- (2) 正しい: クロスエントロピー損失は、分類問題で頻繁に使用される。
- (3) 誤り: MSEは誤差の「二乗」を使うため、負の誤差と正の誤差の符号は考慮されず、すべて正の値になる。
- (4) 正しい: クロスエントロピー損失は確率を前提とするため、ソフトマックス関数と一緒に使われることが多い。
問3: 勾配降下法の仕組み → ✅ 2
解説:
- (1) 誤り: 正しくは「-」で減少させる必要がある。
- (3) 誤り: パラメータを乗算するわけではない。
- (4) 誤り: 除算も間違い。
問4: 勾配降下法の種類 → ✅ 3
解説:
- (1) 正しい: バッチ勾配降下法は、すべてのデータを使用するため計算コストが高い。
- (2) 正しい: ミニバッチ勾配降下法は、全データではなく小さなバッチ単位で学習を行うため、効率が良い。
- (3) 誤り: 確率的勾配降下法(SGD)は、全データではなく「1つのデータ」ごとに学習を行うため、更新が不安定になることもある。
- (4) 正しい: ミニバッチ勾配降下法は、バッチ勾配降下法と確率的勾配降下法の中間的な性質を持つ。
問5: 学習率の影響 → ✅ 3
解説:
(1) 正しい: 学習率が大きすぎると、最適な解を飛び越えてしまい、収束しない可能性がある。
(2) 正しい: 学習率が小さすぎると、更新が少しずつしか進まないため、収束が非常に遅くなる。
(3) 誤り: 学習率は固定でなくてもよく、変化させることで学習を安定させることができる(例: Adamや学習率スケジューリング)。
(4) 正しい: Adamなどの最適化手法では、学習率を適応的に調整しながら学習を進める。
問6: 平均二乗誤差(MSE)の計算

問7: クロスエントロピー損失の計算
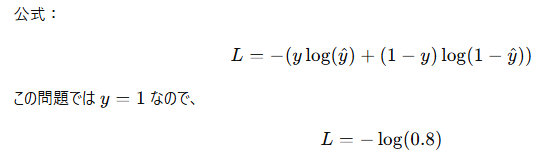
問8: 勾配の計算
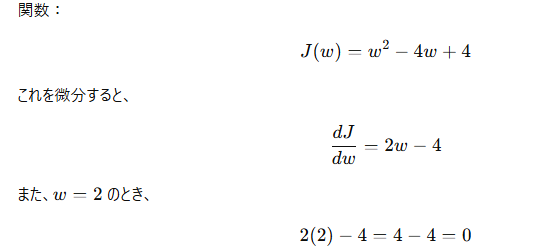
問9: 勾配降下法によるパラメータ更新

参考資料
・データサイエンス数学ストラテジスト[上級]公式テキスト | 公益財団法人 日本数学検定協会 |本 | 通販 | Amazon